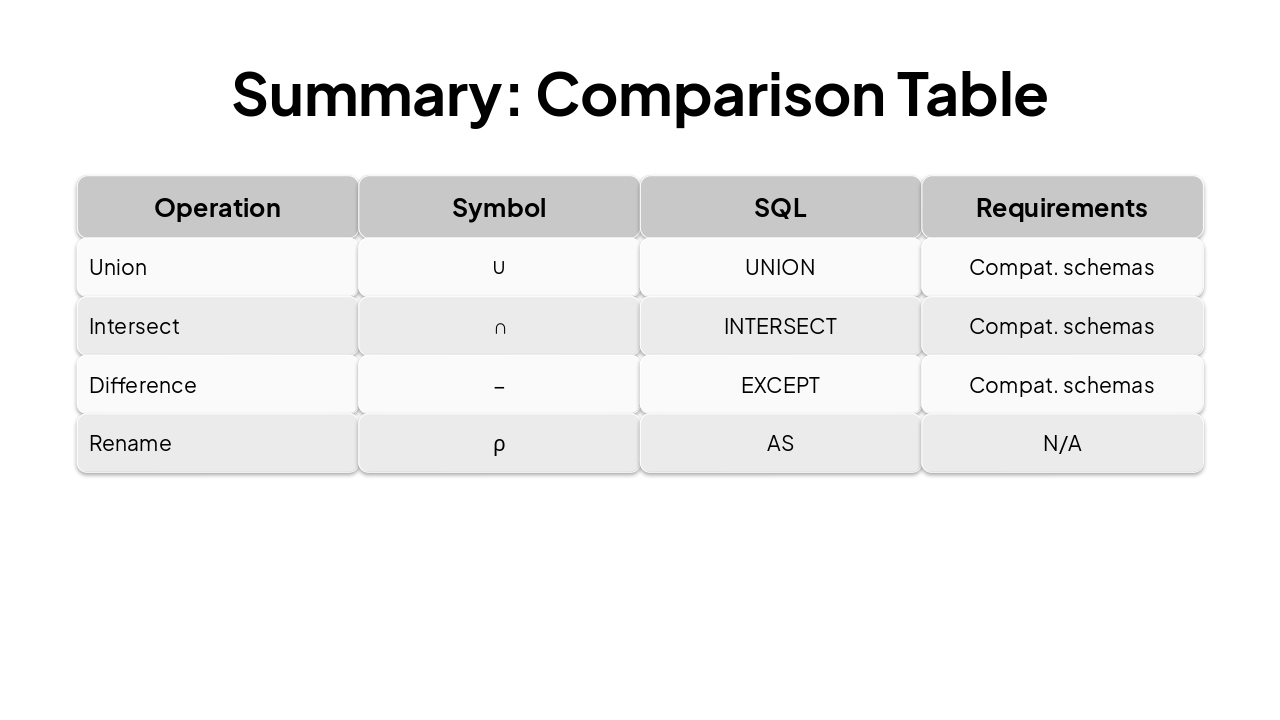
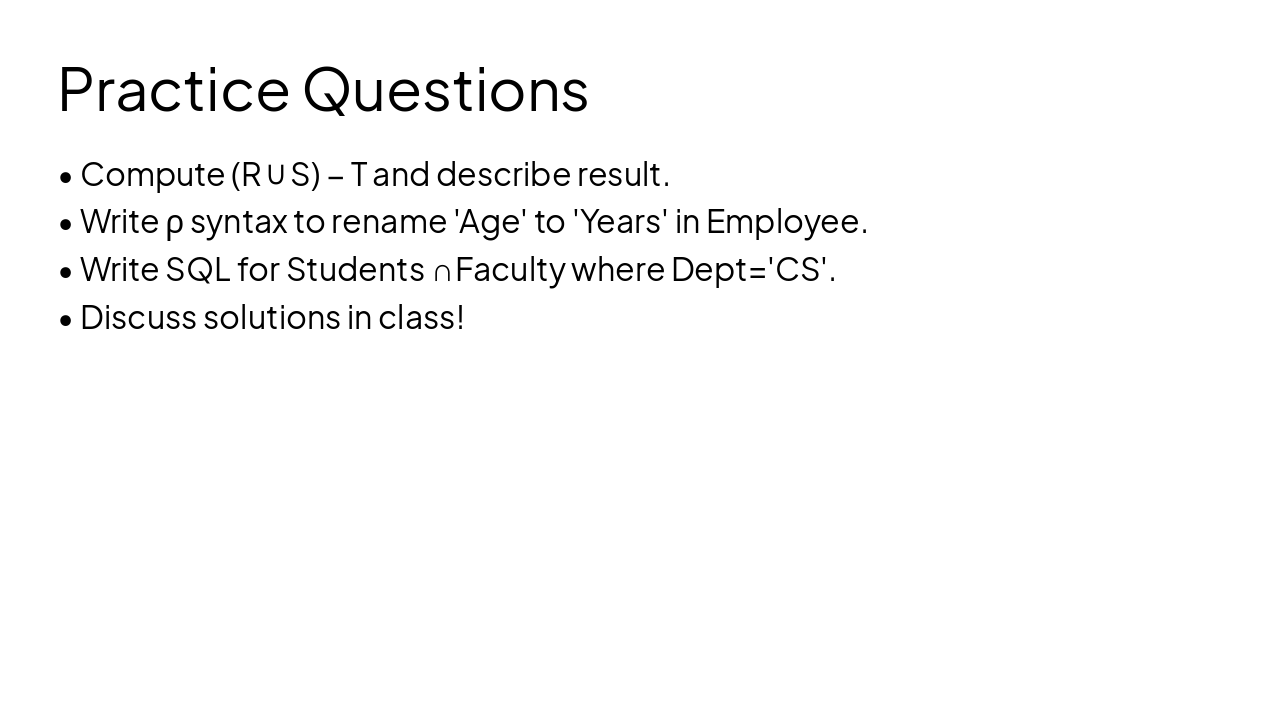
Slide 1 - Set Operations and Renaming in Relational Algebra
This title slide introduces the topic "Set Operations and Renaming in Relational Algebra." It includes the subtitle with instructor "Your Name" and date "October 10, 2024."
Set Operations and Renaming
in Relational Algebra
Instructor: Your Name | Date: October 10, 2024
Source: University-level course presentation